每一個可以努力的日子,都是一份厚禮。
PageRank與社交網絡模型評估(1)
SNS社交網絡在近幾年流行起來,並呈現出火爆的增長趨勢。在仿製國外Facebook、twitter等成功先例的基礎上,國內的人人網、新浪微博等一系列社交網絡正風生水起。
這些社交網站表面上看起來十分普通和其他網站別無二致,但我們可以研究它們背後更深層次的數學原理,從而更有利於推廣營銷。在後面的分析中,我會分別舉例,大家就會明白實際中的應用價值。
我們需要考慮的是怎樣度量一個網絡。網絡其實就是一張圖,圖中有各個節點,節點連接起來,形成邊。在社交網絡中,每個人就是一個節點,人們通過好友關係相互連接。節點是有權重的,就像人具有影響力一樣。
給你一張網絡拓撲圖,你怎樣挖掘這張圖所蘊含的信息呢?你怎樣知道圖中哪一個節點是最重要的?事實上有很多方法,我們自己也可以定義度量的標準。經常用到的有Degree Centrality,Eigenvector Centrality,Katz Centrality,PageRank,Closeness Centrality,Betweenness Centrality,Transitivity……它們從簡單到複雜,從偏重某個屬性到綜合考慮,很多都在現實中合理地使用着,例如PageRank就是Google使用的網頁排名方法。
1. Degree Centrality(節點度)
這是對網絡最為簡單直白的一種度量:僅僅統計每個節點有多少邊。它的現實意義在於有更多邊的節點具有更大的連接性,就像有更多好友的人具有更大的影響力。例如對一個產品做推廣營銷,我們發放免費的試用樣品給消費者,如果消費者滿意他們就會購買,並且推薦給自己的朋友也去購買。這就是口碑影響力。作為廠家,我們當然希望將樣品發放給更具影響力的人,因為他們的一句讚美會傳遞到更多的節點上,為我們帶來更多的潛在客戶。我們知道,圖分為有向圖和無向圖,他們的區別在於節點之間的聯繫是否是雙向的。例如Facebook或者人人網中的好友關係,就是一個無向圖,你是我的好友那麼我也是你的好友;而twitter或者新浪微博則是一個有向圖,因為我“關注”(follow)某些人,又有另外一些人“關注”我,這是一個從一個節點指向另一個節點的關係,不具有可逆性。我們在討論Degree Centrality時,對於有向圖來說,其實有in-degree centrality和out-degree centrality兩種。例如在微博上很多人關注了李開復,也就是說有很多節點指向他,那麼李開復就具有很高的in-degree centrality. 但是要小心,in-degree高的節點不一定是最有價值的,例如在論文參考文獻引用中,一篇文章的in-degree很高表示很多人引用了這篇論文。這篇文章可能提出了一個有價值的研究問題,但是卻犯了明顯的錯誤,於是大家在寫這個研究方向的論文時都會說:“快去圍觀這篇文章,作者太SB了,哈哈哈哈……”
我們希望通過Degree Centrality來找出最有影響力的節點們。問題來了,想要獲得具有Degree Centrality最高的前10個節點,我們需要知道整張圖的結構才行。從數學上講,即需要得到圖的鄰接矩陣A,對於A中的每一行統計有多少個1,最後進行排序取前k個即可得到Degree Centrality值最高的前k個節點。這在實際中並不可行,你並不是Facebook的所有者或者人人網的管理員,你怎麼知道整個社會網絡里誰的好友更多?
2. Eigenvector Centrality(特徵向量)
這是對Degree Centrality的一種改進版。我們希望得到節點重要性的估值,但什麼是重要性?什麼是影響力?在Degree Centrality中,所有的鄰居節點都是平等的。而在實際情況中,不同的鄰居節點可能會有不同的價值。例如我有10個好友,他們都是普通人,而如果有一個人他也有10個好友,但是他的好友都是李嘉誠巴菲特奧巴馬們,顯然,我比不上他,自慚形穢了。
為此我們建立另一種模型:給鄰居節點打分,高分的鄰居會給予我更多積極的影響,使得我的得分也升高。設xi(t)為節點i在t時刻的centrality評估值(得分),centrality值越高說明這個節點越重要。則
或者表示為矩陣形式
其中A為圖的鄰接矩陣。不知道鄰接矩陣?回去複習線性代數離散數學和數據結構吧……
公式(1)比較好理解。基本思想其實就是說,節點j為節點i的鄰居節點(我所說的鄰居意思就是他們有邊相連),在t-1時刻,我們對j疊加求和,意思就是統計節點i的所有鄰居節點的centrality值,然後累加,就是t時刻節點i的centrality值。這個公式對所有節點有效,如果我的鄰居們的centrality值改變了,我的值也會改變,所以這是一個不斷迭代的過程,直到最後所有節點的值在一個閾值內進行可忽略的波動,即收斂。
第二個公式x(0)是0時刻初始化時所有節點的centrality值,它是一個數組。而
不斷迭代就可以得到公式(2)了。
於是x(0)可以看作是A的特徵向量Vi的線性組合,我們可以選取合適的ci使得等式
成立。
結合(2)(3)兩個式子,我們得到
其中ki為矩陣A的特徵值,k1為特徵值中的最大值。
這就是eigenvector centrality。我們如果得到圖A的鄰接矩陣的特徵向量,那麼這個向量x就是所有節點的eigenvector centrality值。我們只需解方程(5)即可。它的一個明顯的屬性就是,xi即節點i的eigenvector centrality,與該節點所有鄰居的eigenvector centrality之和成正比。即
所以,這正解決了我們之前的問題,它將我們鄰居的重要性施加到我們自己身上。有幾種情況會使得xi的值很大,一是節點有很多鄰居,二是它有一個重要鄰居(該鄰居擁有高eigenvector centrality值),或者以上兩種情況同時存在。
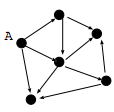
同樣的問題在這裡也存在,那就是我們必須知道圖的鄰接矩陣,也就是整個網絡的拓撲結構。如果網絡中有100萬個節點,我們生成一個100萬×100萬的矩陣也是困難的。另外,還有可能出現下面的情況
這是一個有向圖,注意節點A,它沒有in-degree,也就是說沒有其他節點可以影響到它的centrality值。假如A的centrality值是0,那麼它對它的3個鄰居的貢獻也為0,其中最上面的那個鄰居只有A對它施加影響,於是它的centrality值也為0,最後我們一步步地推斷,會發現整個圖所有節點的centrality值都是0,也就是說圖的鄰接矩陣A=0.這不是我們預想的那樣,因為如果我們希望對網頁做PageRank,這將導致所有頁面的PageRank值都一樣,沒法做排名了。
| 這篇文章由lovelucy於2011-05-02 00:07發表在網絡。你可以訂閱RSS 2.0 也可以發表評論或引用到你的網站。除特殊說明外文章均為本人原創,並遵從署名-非商業性使用-相同方式共享創作協議,轉載或使用請註明作者和來源,尊重知識分享。 |
批評不自由
則讚美無意義


曾哥,你這個咋連一個留言的地方都沒有?當時我也是大愛這個主題風格的說。。。
我才剛上線不到一個月啊,插件神馬的我都還沒摸熟。。。會慢慢完善的。話說訪問速度怎麼樣?