每一个可以努力的日子,都是一份厚礼。
PageRank与社交网络模型评估(1)
SNS社交网络在近几年流行起来,并呈现出火爆的增长趋势。在仿制国外Facebook、twitter等成功先例的基础上,国内的人人网、新浪微博等一系列社交网络正风生水起。
这些社交网站表面上看起来十分普通和其他网站别无二致,但我们可以研究它们背后更深层次的数学原理,从而更有利于推广营销。在后面的分析中,我会分别举例,大家就会明白实际中的应用价值。
我们需要考虑的是怎样度量一个网络。网络其实就是一张图,图中有各个节点,节点连接起来,形成边。在社交网络中,每个人就是一个节点,人们通过好友关系相互连接。节点是有权重的,就像人具有影响力一样。
给你一张网络拓扑图,你怎样挖掘这张图所蕴含的信息呢?你怎样知道图中哪一个节点是最重要的?事实上有很多方法,我们自己也可以定义度量的标准。经常用到的有Degree Centrality,Eigenvector Centrality,Katz Centrality,PageRank,Closeness Centrality,Betweenness Centrality,Transitivity……它们从简单到复杂,从偏重某个属性到综合考虑,很多都在现实中合理地使用着,例如PageRank就是Google使用的网页排名方法。
1. Degree Centrality(节点度)
这是对网络最为简单直白的一种度量:仅仅统计每个节点有多少边。它的现实意义在于有更多边的节点具有更大的连接性,就像有更多好友的人具有更大的影响力。例如对一个产品做推广营销,我们发放免费的试用样品给消费者,如果消费者满意他们就会购买,并且推荐给自己的朋友也去购买。这就是口碑影响力。作为厂家,我们当然希望将样品发放给更具影响力的人,因为他们的一句赞美会传递到更多的节点上,为我们带来更多的潜在客户。我们知道,图分为有向图和无向图,他们的区别在于节点之间的联系是否是双向的。例如Facebook或者人人网中的好友关系,就是一个无向图,你是我的好友那么我也是你的好友;而twitter或者新浪微博则是一个有向图,因为我“关注”(follow)某些人,又有另外一些人“关注”我,这是一个从一个节点指向另一个节点的关系,不具有可逆性。我们在讨论Degree Centrality时,对于有向图来说,其实有in-degree centrality和out-degree centrality两种。例如在微博上很多人关注了李开复,也就是说有很多节点指向他,那么李开复就具有很高的in-degree centrality. 但是要小心,in-degree高的节点不一定是最有价值的,例如在论文参考文献引用中,一篇文章的in-degree很高表示很多人引用了这篇论文。这篇文章可能提出了一个有价值的研究问题,但是却犯了明显的错误,于是大家在写这个研究方向的论文时都会说:“快去围观这篇文章,作者太SB了,哈哈哈哈……”
我们希望通过Degree Centrality来找出最有影响力的节点们。问题来了,想要获得具有Degree Centrality最高的前10个节点,我们需要知道整张图的结构才行。从数学上讲,即需要得到图的邻接矩阵A,对于A中的每一行统计有多少个1,最后进行排序取前k个即可得到Degree Centrality值最高的前k个节点。这在实际中并不可行,你并不是Facebook的所有者或者人人网的管理员,你怎么知道整个社会网络里谁的好友更多?
2. Eigenvector Centrality(特征向量)
这是对Degree Centrality的一种改进版。我们希望得到节点重要性的估值,但什么是重要性?什么是影响力?在Degree Centrality中,所有的邻居节点都是平等的。而在实际情况中,不同的邻居节点可能会有不同的价值。例如我有10个好友,他们都是普通人,而如果有一个人他也有10个好友,但是他的好友都是李嘉诚巴菲特奥巴马们,显然,我比不上他,自惭形秽了。
为此我们建立另一种模型:给邻居节点打分,高分的邻居会给予我更多积极的影响,使得我的得分也升高。设xi(t)为节点i在t时刻的centrality评估值(得分),centrality值越高说明这个节点越重要。则
或者表示为矩阵形式
其中A为图的邻接矩阵。不知道邻接矩阵?回去复习线性代数离散数学和数据结构吧……
公式(1)比较好理解。基本思想其实就是说,节点j为节点i的邻居节点(我所说的邻居意思就是他们有边相连),在t-1时刻,我们对j叠加求和,意思就是统计节点i的所有邻居节点的centrality值,然后累加,就是t时刻节点i的centrality值。这个公式对所有节点有效,如果我的邻居们的centrality值改变了,我的值也会改变,所以这是一个不断迭代的过程,直到最后所有节点的值在一个阈值内进行可忽略的波动,即收敛。
第二个公式x(0)是0时刻初始化时所有节点的centrality值,它是一个数组。而
不断迭代就可以得到公式(2)了。
于是x(0)可以看作是A的特征向量Vi的线性组合,我们可以选取合适的ci使得等式
成立。
结合(2)(3)两个式子,我们得到
其中ki为矩阵A的特征值,k1为特征值中的最大值。
这就是eigenvector centrality。我们如果得到图A的邻接矩阵的特征向量,那么这个向量x就是所有节点的eigenvector centrality值。我们只需解方程(5)即可。它的一个明显的属性就是,xi即节点i的eigenvector centrality,与该节点所有邻居的eigenvector centrality之和成正比。即
所以,这正解决了我们之前的问题,它将我们邻居的重要性施加到我们自己身上。有几种情况会使得xi的值很大,一是节点有很多邻居,二是它有一个重要邻居(该邻居拥有高eigenvector centrality值),或者以上两种情况同时存在。
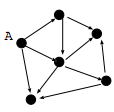
同样的问题在这里也存在,那就是我们必须知道图的邻接矩阵,也就是整个网络的拓扑结构。如果网络中有100万个节点,我们生成一个100万×100万的矩阵也是困难的。另外,还有可能出现下面的情况
这是一个有向图,注意节点A,它没有in-degree,也就是说没有其他节点可以影响到它的centrality值。假如A的centrality值是0,那么它对它的3个邻居的贡献也为0,其中最上面的那个邻居只有A对它施加影响,于是它的centrality值也为0,最后我们一步步地推断,会发现整个图所有节点的centrality值都是0,也就是说图的邻接矩阵A=0.这不是我们预想的那样,因为如果我们希望对网页做PageRank,这将导致所有页面的PageRank值都一样,没法做排名了。
| 这篇文章由lovelucy于2011-05-02 00:07发表在网络。你可以订阅RSS 2.0 也可以发表评论或引用到你的网站。除特殊说明外文章均为本人原创,并遵从署名-非商业性使用-相同方式共享创作协议,转载或使用请注明作者和来源,尊重知识分享。 |
批评不自由
则赞美无意义


曾哥,你这个咋连一个留言的地方都没有?当时我也是大爱这个主题风格的说。。。
我才刚上线不到一个月啊,插件神马的我都还没摸熟。。。会慢慢完善的。话说访问速度怎么样?